180З годъ. Августъ.
Августа 7 го по полуночи въ 9 часовъ перемѣнился вѣтръ отъ SW къ StO, и въ 10 находились мы уже подъ парусами. Въ сіе время прибылъ на корабль Адмиралъ Ханыковъ, пожелать намъ щастія и проводилъ насъ до брантвахты, стоявшей на якоряхъ въ 4 хъ миляхъ отъ Кронштата…
Так начинается вторая глава знаменитой книги «ПУТЕШЕСТВІЕ ВОКРУГЪ СВѢТА въ 1803, 4, 5 и 1806 годахъ. По повелѣнію ЕГО ИМПЕРАТОРСКАГО ВЕЛИЧЕСТВА АЛЕКСАНДРА ПЕРВАГО, на корабляхъ НАДЕЖДѢ и НЕВѢ, подъ начальствомъ Флота Капитанъ Лейтенанта, нынѣ Капитана втораго ранга, Крузенштерна, Государственнаго Адмиралтейскаго Департамента и ИМПЕРАТОРСКОЙ Академіи Наукъ Члена.»
Шлюп «Нева»
«…День былъ самый прекрасный и теплый, термометръ показывалъ 17 град., но не взирая на то надобно было ожидать худой погоды: ибо морскій барометръ опустился въ нѣсколько часовъ на 4 линіи, а имянно отъ 29,90 на 29,50. Въ полдень Толбухинъ маякъ находился отъ насъ NO 74°, разстояніемъ на одну милю; въ 8 часовъ вечера маякъ острова Сескара былъ отъ насъ SW 20°. Въ 10 часовъ сдѣлался свѣжій вѣтръ отъ SW, который принудилъ насъ лавировать цѣлую ночь; на другій день вѣтръ усилился и дулъ при пасмурной погодѣ отъ SW и W такъ, что ходъ нашъ былъ очень не успѣшенъ, и мы, находясь въ виду острова Гогланда, не могли обойти онаго. 10 го числа вѣтръ утихъ, и погода сдѣлалась опять прекрасная; въ полдень по наблюденію широта 60°.3′.39″., долгота по хронометру восточная 26°.58′.15″., считая отъ меридіана Гринвичской обсерваторіи. Въ два часа по полудни обошли мы островъ Гогландъ. 11 го бралъ я многократно лунныя разстоянія, изъ которыхъ, вывелъ долготу въ полдень 26°.48,00; по хронометрамъ же была оная 26°.41′.19″…»
Обратите внимание, что Крузенштерн упоминает «лунные расстояния», которые он «брал» и из которых вывел долготу. Надо сказать, что лунные расстояния упоминаются в книге очень часто.
«…Декабря 4 го, сдѣланы были мною два вычисленія по взятіи лунныхъ разстояній, коихъ среднее показало долготу въ полдень 31°,15′ по наблюденіямъ Доктора Горнера была оная 5 минутами восточнѣе. Склоненіе магнитной стрѣлки по учиненнымъ многимъ наблюденіямъ вышло 3°,01′ западное; южное наклоненіе оной найдено на другой день 39°,00′, подъ широтою 16°, 42′ и долготою 31°,40′. Взятыя, многія лунныя разстоянія показали того дня западную долготу нашу 31°,50′,45″. 7 го подъ 19°,57′ широты, 32°,12′ долготы, найдено южное наклоненіе магнитной стрѣлки 36°, 48’…»
И.Ф. Крузенштерн – человек и пароход
Итак, Иван Федорович Крузенштерн использовал метод лунных расстояний определения долготы. В чем суть этого метода? В современных учебниках по навигации о нем нет ни слова. Давайте разбираться.
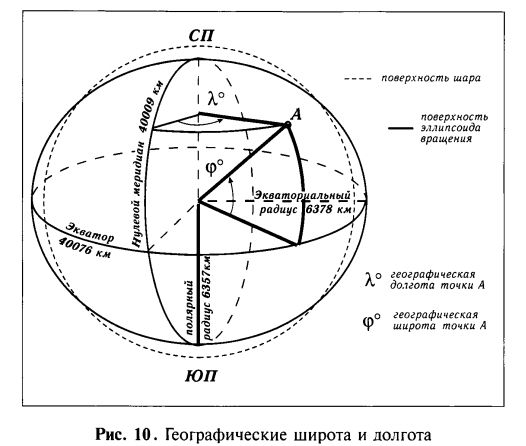
Понятия географических широты и долготы, определяющих местоположение какого-либо пункта на поверхности Земли, вероятно, возникли в древней Греции за 300 лет до нашей эры, но не в том виде, как мы понимаем их сейчас: сегодня широта — это количество градусов к северу или к югу от экватора, а долгота — количество градусов к востоку или к западу от некоторого выбранного меридиана. В эллинские времена эти величины наиболее часто, хотя и не всегда, выражали в интервалах времени: так, широту определенного пункта определяли продолжительностью самого длинного светового дня в году, разность долгот между двумя пунктами-различием их местных времен.
Как известно, разность долгот двух точек на земной поверхности равна разности значений местного времени в этих точках в один и тот же физический момент (который определялся по наблюдению какого-либо астрономического явления). Таким образом, задача определения долготы сводится к получению в некоторый момент разности значений местного времени в определяемом пункте и пункте, долгота которого известна.
Уже во времена Гиппарха (II век до нашей эры) стало ясно, что определение разности долгот двух пунктов возможно по наблюдению (т.е. измерению местного времени) момента некоторого события в каждом из этих пунктов. В качестве такого события Гиппарх предложил использовать затмения Луны, так как ее вхождение в тень Земли и есть то событие, которое происходит в один и тот же момент для всех наблюдателей, где бы они ни находились на земной поверхности. Но, к сожалению, Гиппарх не указал способов, как измерить местное время в каждом из пунктов наблюдения. Непосредственно использовать для этой цели солнечные часы было невозможно, так как во время лунного затмения Солнце находится ниже горизонта.
Лунное затмение
При определении долготы методом лунного затмения возникали и другие трудности. Затмения случаются довольно редко: два-три раза в год, а иногда и совсем не происходят, поэтому определение долгот для большого числа пунктов требует длительного времени, а для мореплавателей иметь потенциальную возможность определить долготу пару раз в год по затмению – совсем не вариант.
Справедливости ради следует отметить, что в качестве «небесных часов» могут использоваться не только лунные затмения, но и затмения солнца. Это было известно средневековым астрономам. С изобретением телескопа Галилео Галилеем, стало возможным использовать для этих целей прохождение спутников Юпитера на фоне планеты, которое открыл Галилей, или прохождение Венеры через Солнечный диск. Однако все эти способы имели непреодолимые в те времена технические и методические сложности.
Потребовалось полтора тысячелетия после Гиппарха для того, чтобы наконец решить эту проблему. В 1514 г. Иоганн Вернер (1468-1522) из Нюрнберга предложил впредь для определения долготы воспользоваться новым методом, названным им методом лунных расстояний.
Иоганн Вернер
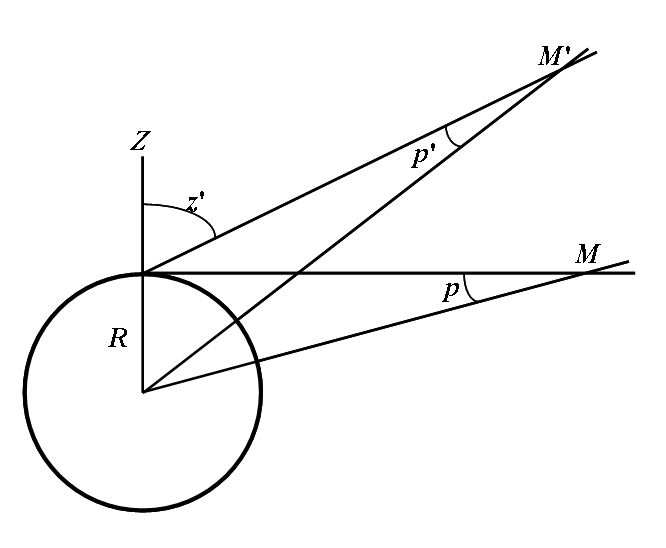
В течение месяца Луна совершает один полный оборот вокруг Земли с запада на восток — в направлении, противоположном движению звезд. Она проходит приблизительно 0,5°, или путь, равный ее диаметру, за 1 ч. Это относительно быстрое движение Луны и навело Вернера на мысль использовать Луну как гигантские небесные часы, где сама Луна будет служить часовой стрелкой, а зодиакальные звезды-цифрами циферблата.
Наблюдатель, находящийся на Земле, каждую ночь видит, как звезды движутся по небесному своду с востока на запад со скоростью более чем 15° в час, тогда как Луна за то же время проходит около 14,5°. Таким образом, Луна отстает от звезд на 0,5° в час, поэтому зодиакальная звезда, опережающая Луну, скажем, на 40° в 22.00, в полночь будет находиться впереди нее на 41° (так как Луна пройдет за это время 29°, а звезда 30°). Вернер предположил, что в определенный момент «лунное расстояние» между зодиакальной звездой и Луной должно быть одинаковым для любого наблюдателя, в какой бы географической точке он ни находился, поэтому изменение лунного расстояния можно использовать для измерения времени на некотором данном, меридиане (впредь мы будем принимать за него, например, гринвичский). Этим же методом можно воспользоваться и для определения долготы, сравнивая предсказанные расстояния Луны по отношению к звездам, и действительные расстояния, измеренные навигатором с необходимой степенью точности.
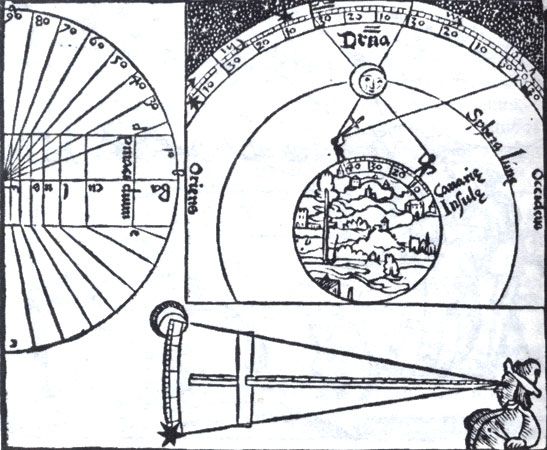
Наблюдения с помощью поперечного жезла, используемые для определения лунных расстояний и измерения высот зданий. Эта гравюра была приведена на титуле труда Петра Апиана ‘Введение в географию’ (Introductio Geographica Petri Apiani in Doctissimus Verneri Annotationes…), Ингольштадт, 1533. (Британская библиотека.)
Морякам и ученым метод лунных расстояний был известен не в том виде, как он описывался Вернером, — они знали его наглядное, как хорошая картина, описание, приведенное в «Космографии» (Ингольштадт, 1524) Петра Апиана (1495-1552)
Древний рисунок, иллюстрирующий определение долготы методом лунных расстояний, из первого издания труда Петра Апиана ‘Космография’ (Инголыптадт и Ландшат, 1524). (Бодлеанская библиотека, Оксфорд.)
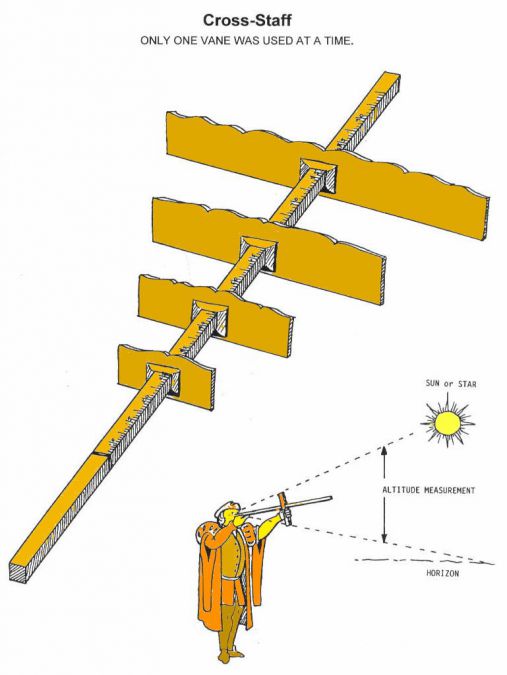
«Я открою вам, какие три вещи необходимы для этого дела. Первое-это астрономический жезл, называемый также жезлом Якоба (подобный которому вы можете найти среди других инструментов), второе — истинное положение Луны в поясе Зодиака в градусах и минутах в тот момент, когда вы производите наблюдение (его можно взять из эфемерид), и третье — долгота опорной звезды, которую можно получить из таблицы опорных звезд, помещенной в моей первой книге. Имея все это, вы должны взять ваш стержень с прикрепленной к нему поперечной рейкой и навести один конец рейки на центр Луны, а другой — на подходящую звезду, затем передвигать рейку вверх и вниз до тех пор, пока концы стержня не соединят центры Луны и звезды. После этого рейка укажет вам расстояние Луны от звезды в градусах и минутах. Зная расстояние в градусах и минутах между Луной и опорной звездой, которое вы имели до наблюдения, и вычьтя эти расстояния одно из другого, вы получите разность. Если вы поделите эту разность на величину, на которую перемещается Луна за один час, то это даст вам момент, когда Луна находилась за звездой (если звезда расположена к западу от нее), или когда она будет перед звездой, если звезда была восточнее Луны».
Из книги Петра Апиана «Космография»
Астрономический жезл
Предположение Вернера о том, что положение Луны на небе не зависит от географического положения наблюдателя, ошибочно. Штурману обычно приходилось прибегать к довольно утомительным арифметическим вычислениям, чтобы учесть параллакс (изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя) и различные рефракционные эффекты, влияющие на видимые положения двух небесных тел, имеющих разные высоты.
Параллакс
Теоретически метод Вернера был обоснован, хотя для выполнения практической работы требовались следующие условия: знание точных положений звезд относительно друг друга; возможность заранее предсказывать положение Луны по отношению к звездам (эти предсказанные положения штурман должен иметь перед отправлением в плавание, которое может продолжаться несколько лет), а также инструмент для проведения наблюдений с требуемой степенью точности. Прошло 250 лет, прежде чем эти требования удалось удовлетворить.
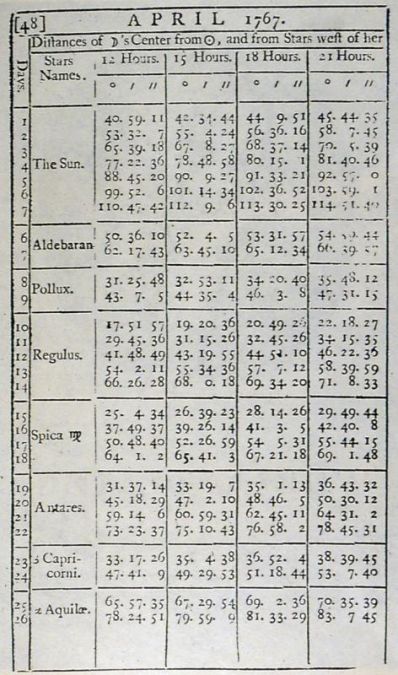
Возможность практического применения метода лунных расстояний была получена в 1760-х гг., когда с публикацией «Морского альманаха» было обеспечено выполнение первых двух условий. В альманахе приводились таблицы расстояний от Луны до Солнца и некоторых зодиакальных звезд на каждые три часа для всего года.
Страница «Nautical Almanac» на 1767 год с таблицей лунных расстояний
Третье условие было выполнено с изобретением секстана
Короче говоря, при использовании метода лунных расстояний было необходимо произвести три одновременных или почти одновременных наблюдения: углового расстояния между Луной и звездой или Солнцем, высоты Луны и высоты звезды или Солнца; время при этом должно было отсчитываться по самым совершенным из имевшихся в то время часам. Этот метод успешно мог применяться при полностью видимом горизонте (в дневное время или в сумерки), но это условие было не столь существенно, так как при наблюдениях высот не требовалась слишком высокая точность — достаточно было просто хоть как-то видеть горизонт. Наблюдения и обработка результатов производились следующим образом.
А. Определение местного времени в наблюдательном пункте путем измерения высоты Солнца или звезды, лучше всего в тот же самый момент, когда измерялось лунное расстояние. Если же горизонт был закрыт, можно было воспользоваться значением высоты, определенной накануне вечером или на следующее утро, учитывая при этом сдвиг во времени. Местное время относительно просто определялось путем расчетов с применением сферической тригонометрии.
Б. Определение лунного расстояния с учетом эффектов параллакса и рефракции. Для этого существовали таблицы, но вычисления были довольно трудоемкими. В результате получали исправленное расстояние между центром Луны и центром Солнца или звезды, такое, каким его можно было бы видеть из центра Земли. Для получения этих данных и были составлены таблицы «Морского альманаха».
В. Определение гринвичского времени из наблюдений. С помощью таблиц альманаха производилась интерполяция исправленного лунного расстояния, полученного на этапе Б.
Так, примерно в 04.30 астрономического времени (16.30 гражданского) 4 октября 1772 г. Уильям Уэйлс, астроном, принимавший участие в экспедиции капитана Кука по Южной Атлантике на корабле «Резолюшн», произвел по пути от Плимута к мысу Доброй Надежды четыре последовательных измерения лунных расстояний. Он наблюдал лимбы (края) Солнца и Луны и после усреднения отсчетов получил лунное расстояние 102° 26’55». Исправленное лунное расстояние (этап Б) равнялось 102°36’08». Затем после интерполирования по «Морскому альманаху», где были приведены данные для 6 и 9 ч было определено гринвичское время наблюдения — 6 ч 23 мин 39 с.
Страница альманаха, откуда были получены значения лунных расстояний Уильямом Уэйлсом
Г. Определение долготы по разности местного времени, найденного на этапе А, и гринвичского времени, найденного на этапе В. Таким образом, для нашего случая получаем:
что соответствует 29° 11′ з. д.
В настоящее время, с изобретением высокоточных хронометров, а несколько позднее, и радиосвязи, метод определения долготы через лунные расстояния утратил свою актуальность и был исключен из учебников навигации. Тем не менее, благодаря этому методу мореплаватели нескольких эпох смогли определить и нанести на карты множество открытых ими земель.
Источники:
«Гринвичское время и открытие долготы.» (Greenwich time and the discovery of the longitude, 1980) Хауз Д., Перевод с английского М.И.Малышева. Под редакцией и с предисловием В.В.Нестерова. Издательство «Мир», Москва
DEREK HOUSE «GREENWICH TIME and the discovery of the longitude» Oxford; New York : Oxford University Press, 1980.